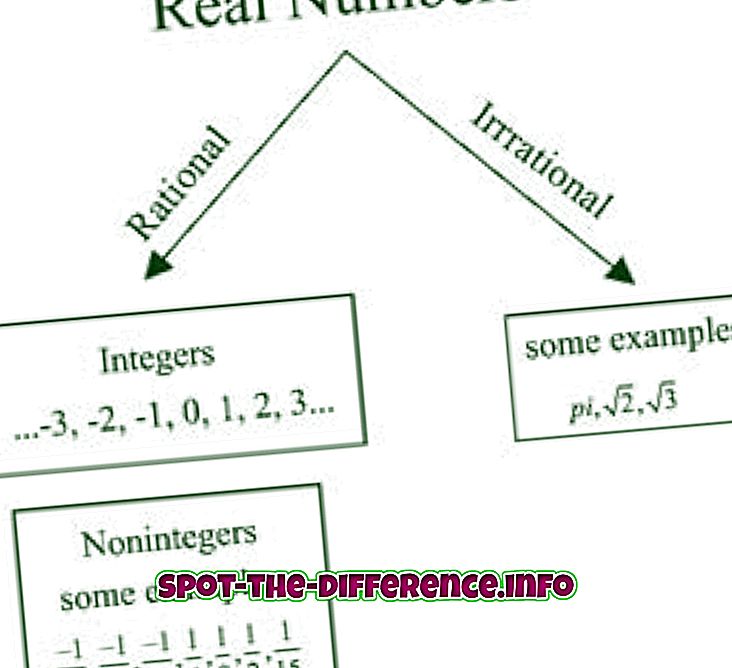
Schlüsseldifferenz: Eine reelle Zahl ist eine Zahl, die einen beliebigen Wert in der Zahlenzeile annehmen kann. Eine reelle Zahl kann eine der rationalen und irrationalen Zahlen sein. Komplexe Zahlen sind die Zahlen, die in der Form von a + ib existieren, wobei a und b reelle Zahlen und i einen Imaginärteil bedeuten.

Es ist wichtig, das Konzept der Zahlenzeile zu verstehen, um echte Zahlen zu lernen. Die Zahlenlinie kann als tatsächliche geometrische Linie ausgedrückt werden, wobei ein Punkt als Ursprung ausgewählt wird. Punkte, die auf der rechten Seite des Ursprungs liegen, werden als positive Zahlen betrachtet, während Zahlen, die auf der linken Seite des Ursprungs liegen, als negativ betrachtet werden. Eine reelle Zahl bezieht sich auf eine beliebige Nummer, die in dieser Nummernzeile zu finden ist. Sie bestehen daher aus ganzen (0, 1, 3, 9, 26), rationalen (6/9, 78, 98) und irrationalen Zahlen (Quadratwurzel von 3, pi). Die Unendlichkeit fällt nicht in die Kategorie der reellen Zahlen. Die Quadratwurzel von -1 ist auch keine reelle Zahl und wird daher als imaginäre Zahl bezeichnet.

Komplexe Zahlen gelten als Erweiterung des reellen Zahlensystems. Sie wurden entwickelt, um die Probleme zu lösen, die nicht mit reellen Zahlen gelöst werden können. Komplexe Zahlen kombinieren tatsächlich reelle und imaginäre Zahlen (a + ib), wobei a und b reelle Zahlen sind, während i eine imaginäre Zahl bezeichnet. Definitionsgemäß sind imaginäre Zahlen jene Zahlen, die, wenn sie quadriert werden, ein negatives Ergebnis ergeben. Diese Aussage würde nicht viel Logik ausmachen, denn wenn wir das Quadrat einer positiven Zahl berechnen, erhalten wir ein positives Ergebnis. Wenn eine negative Zahl quadriert wird, liefert sie ebenfalls eine positive Zahl. Daher wird solchen Zahlen ein imaginärer Name gegeben. Die imaginäre Einheitszahl wird jedoch als Quadratwurzel von -1 betrachtet.

Vergleich zwischen reeller Zahl und komplexer Zahl:

	Reelle Zahl	Komplexe Zahl
Definition	Eine reelle Zahl ist eine Zahl, die einen beliebigen Wert in der Zahlenzeile annehmen kann. Sie können jede der rationalen und irrationalen Zahlen sein.	Komplexe Zahlen gelten als Erweiterung des reellen Zahlensystems. Komplexe Zahlen kombinieren tatsächlich reelle und imaginäre Zahlen (a + ib), wobei a und b reelle Zahlen sind, während i eine imaginäre Zahl bezeichnet.
Zahlenzeile	Kann in die Zahlenzeile eingetragen werden.	Kann nicht in der Zahlenzeile dargestellt werden.
Enthält	Dies schließt positive und negative Werte, ganze Zahlen und rationale Zahlen, Quadratwurzeln, Kubikwurzeln, π (pi) usw. ein, ist aber nicht darauf beschränkt.	Dies beinhaltet Zahlen wie 3 - 2i oder 5 + √6i, da sie als Summe oder Differenz einer reellen Zahl und einer imaginären Zahl geschrieben werden können.
Symbol	R	C
Mitglieder	Alle reellen Zahlen sind auch komplexe Zahlen mit Null für den Imaginärteil.	Alle imaginären Zahlen sind auch komplexe Zahlen mit Null für den Realteil.