Hauptunterschied: Ein Kreis und eine Ellipse haben geschlossene geschwungene Formen. In einem Kreis sind alle Punkte gleich weit vom Zentrum entfernt, was bei einer Ellipse nicht der Fall ist. In einer Ellipse befinden sich alle Punkte in unterschiedlichen Abständen vom Zentrum.

Mathematisch ist ein Kreis eine Hauptform im Bereich der Geometrie und deren Definitionszustände: Ein Kreis ist eine Form, bei der sich alle Punkte im gleichen Abstand vom Mittelpunkt befinden. Es ist nach seinem Zentrum benannt. Einige Beispiele aus der realen Welt eines Kreises sind Räder, ein Speiseteller und eine Münze.

Das Wort " Zirkus " leitet sich von dem griechischen Begriff " Kirkos " ab, der eine Metathese des homerischen Griechen ist und " Reifen " oder " Ring " bedeutet. Der Kreis war schon vor der aufgezeichneten Geschichte bekannt. Die Sonne und der Mond sind natürliche Beispiele für einen Kreis, während selbst ein kurzer Wind im Wind die Form eines Kreises im Sand bildet. Das Prinzip eines Kreises wurde vom Urmenschen bei der Bildung von Rädern und Zahnrädern angewendet. In der Neuzeit gibt es eine Vielzahl von Maschinen, die auf der Kreisform basieren. Das Studium eines Kreises und seiner Entwicklung ist in den Bereichen Mathematik, Geometrie, Astronomie und Analysis anwendbar.

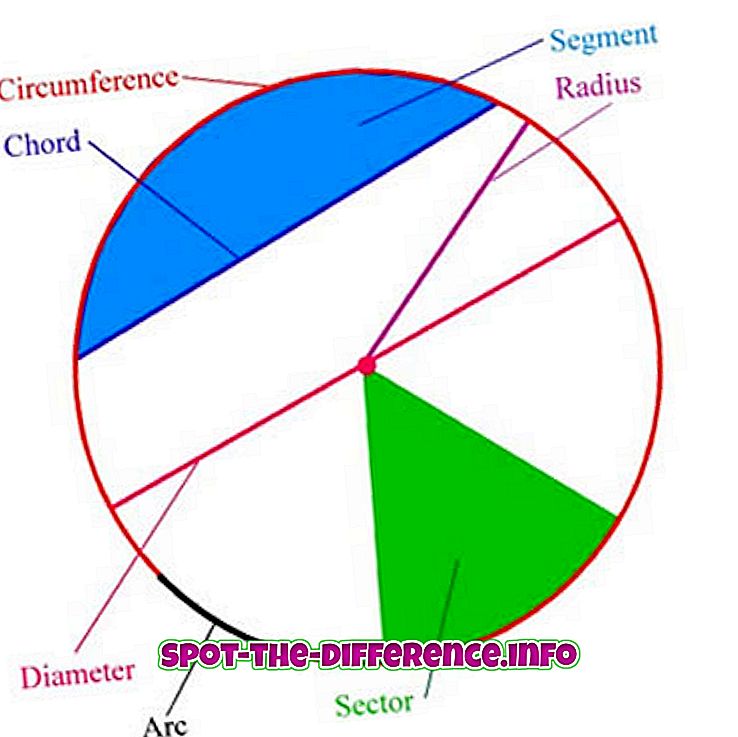
Die folgenden Begriffe sind in der Kreisterminologie enthalten:

Bogen : jeder zusammenhängende Teil des Kreises.

Mitte : der Punkt, der von den Punkten auf dem Kreis gleich weit entfernt ist.

Radius : ein Liniensegment, das den Mittelpunkt des Kreises mit einem beliebigen Punkt auf dem Kreis selbst verbindet; oder die Länge eines solchen Segments, das einen halben Durchmesser hat.

Durchmesser : ein Liniensegment, dessen Endpunkte auf dem Kreis liegen und das durch die Mitte verläuft; oder die Länge eines solchen Liniensegments, das die größte Entfernung zwischen zwei Punkten auf dem Kreis ist. Es ist ein Spezialfall eines Akkords, nämlich der längste Akkord, und es ist der doppelte Radius.

Umkreis: Die Länge eines Kreises entlang des Kreises.

Akkord : ein Liniensegment, dessen Endpunkte auf dem Kreis liegen.

Tangente : Eine koplanare gerade Linie, die den Kreis an einem Punkt berührt.

Halbkreis : Eine Region, die durch einen Durchmesser und einen Bogen begrenzt ist, der zwischen den Endpunkten des Durchmessers liegt. Es ist ein Sonderfall eines Kreissegments, nämlich das größte.

Kreissektor : Ein Bereich, der von zwei Radien begrenzt wird, und einem Bogen, der zwischen den Radien liegt.

Mathematisch ist eine Ellipse eine übliche Form in der Mathematik. Seine Definition besagt: Eine gekrümmte Linie, die eine geschlossene Schleife bildet, wobei die Summe der Abstände von zwei Punkten (Brennpunkten) zu jedem Punkt der Linie konstant ist. Die realen Beispiele einer Ellipse sind: ein Hula-Hoop-Reifen, ein Glas Wasser und ein einfacher Teller, wenn er geneigt ist, um aus einem Winkel zu sehen.

Apollonius von Perga gab in seinen Conics den Namen "Ellipse" an, der die Verbindung einer Kurve mit der Anwendung von Flächen betont. Es ist eine Kurve in einer Ebene, die zwei Brennpunkte umgibt, so dass eine gerade Linie, die von einem Brennpunkt zu einem beliebigen Punkt der Kurve und dann zurück zum anderen Brennpunkt gezogen wird, für jeden Punkt der Kurve die gleiche Länge hat. Seine Form wird durch seine Exzentrizität dargestellt, die willkürlich nahe bei 1 liegt. Das Studium der Ellipse und ihrer Eigenschaften ist allgemein auf Physik, Astronomie und Ingenieurwissenschaften anwendbar. Die Umlaufbahnen der Planeten mit der Sonne an einem der Brennpunkte, die die Planeten umkreisenden Monde und andere Systeme mit zwei astronomischen Körpern sind die allgemeinen Beispiele für elliptische Bahnen. Die Form von Planeten und Sternen wird oft durch Ellipsoide beschrieben. Die Ellipse wird auch als die einfachste Lissajous-Figur betrachtet, die gebildet wird, wenn die horizontalen und vertikalen Bewegungen Sinusoide mit der gleichen Frequenz sind.

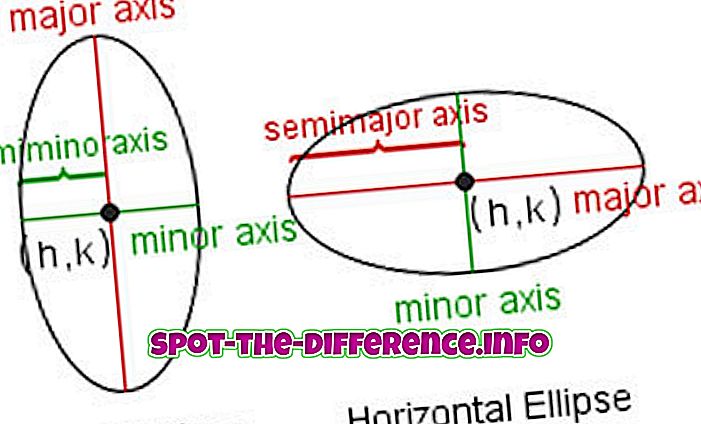
Die Begriffe, die hauptsächlich in die Terminologie der Ellipse involviert sind, lauten:

Fokus : Die Entfernung vom Zentrum und wird in Bezug auf die Haupt- und Nebenradien ausgedrückt.

Exzentrizität : Die Exzentrizität der Ellipse (üblicherweise als e oder ε bezeichnet) wird in Ausdrücken unter Verwendung des Abflachungsfaktors ausgedrückt.

Directrix : Dies ist eine Linie, die parallel zur Nebenachse verläuft und mit der jeder Fokus verknüpft ist.

Latus rectum : Die Akkorde einer Ellipse, die senkrecht zur Hauptachse stehen und durch einen ihrer Brennpunkte verlaufen, werden Latus rectum der Ellipse genannt.

Major / Minor-Achse : Der längste und kürzeste Durchmesser einer Ellipse. Die Länge der Hauptachse entspricht der Summe der beiden Generatorzeilen.

Semi-Dur / Semi-Moll-Achse : Der Abstand vom Zentrum zum am weitesten entfernten Punkt der Ellipse. Die Hälfte der Haupt- / Nebenachse.

Akkorde : Die Mittelpunkte einer Gruppe paralleler Akkorde einer Ellipse sind kollinear.

Umfang : Er ist mit der Länge der großen Achse und der Exzentrizität verbunden und ist Bestandteil einer Ellipse.

Vergleich zwischen Circle und Ellipse: