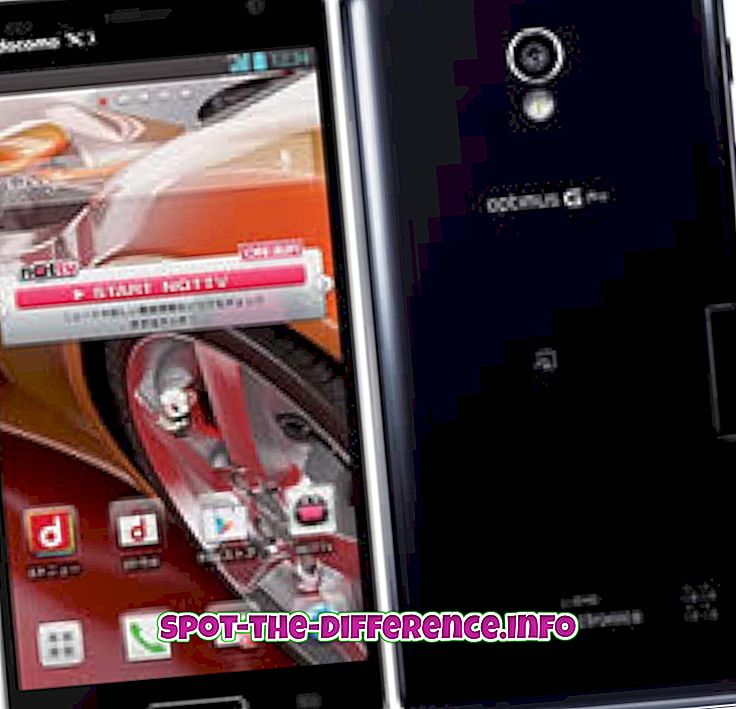
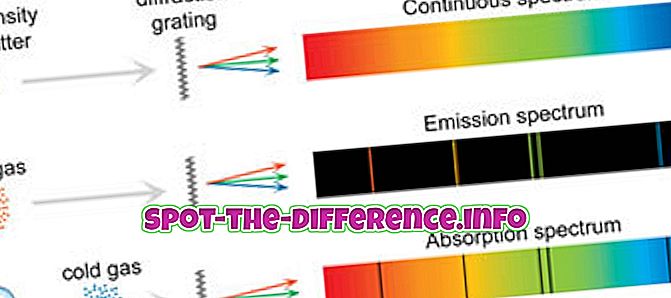
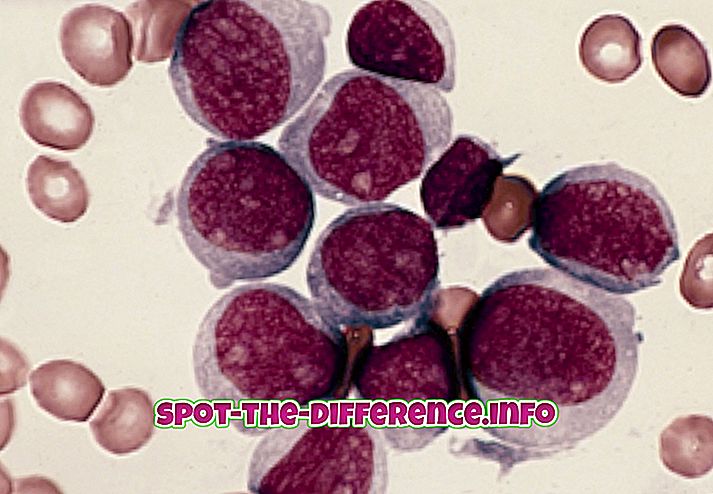
Hauptunterschied: Eine Parabel ist ein konischer Abschnitt, der erstellt wird, wenn eine Ebene eine konische Fläche parallel zur Seite des Kegels schneidet. Eine Hyperbel entsteht, wenn eine Ebene eine konische Fläche parallel zur Achse schneidet.

Parabel und Hyperbel sind zwei verschiedene Wörter, Abschnitte und Gleichungen, die in der Mathematik verwendet werden, um zwei verschiedene Abschnitte eines Kegels zu beschreiben. Diese unterscheiden sich in Form, Größe und verschiedenen anderen Faktoren bei der Verwendung von Formeln, die zur Berechnung verwendet werden. Um sie zu verstehen, sollten wir zuerst den Kegel und die verschiedenen konischen Abschnitte verstehen.

Ein konischer Schnitt ist eine Kurve, die sich ergibt, wenn sich eine Ebene auf verschiedene Weise mit einem Kegel schneidet. Die Schnitte, die aus der Schnittmenge erhalten werden, umfassen Ellipse, Kreis, Parabel und Hyperbel. Gemäß der analytischen Geometrie wird konisch definiert als „ebene algebraische Kurve von Grad 2“. Die gängige Definition des konischen Abschnitts umfasst einen Fokuspunkt, eine Directrix-Linie und eine Exzentrizität. Es wird erwartet, dass der Fokuspunkt und die Directrix-Linien in einer Kegelform fest sind. Das Verhältnis wird als Exzentrizität des Kegelschnittes bezeichnet. Die Exzentrizität von Ellipsen, Parabeln und Hyperbeln unterscheidet sich; Ellipsen haben eine Exzentrizität von weniger als 1, Parabeln haben eine Exzentrizität von 1 und Hyperbeln haben eine Exzentrizität von mehr als 1. Die frühesten bekannten Arbeiten an konischen Abschnitten können von Menaechmus, der einen Weg entdeckte, auf das vierte Jahrhundert v. Chr. datiert werden um das Problem der Verdoppelung des Würfels durch die Verwendung von Parabeln zu lösen.

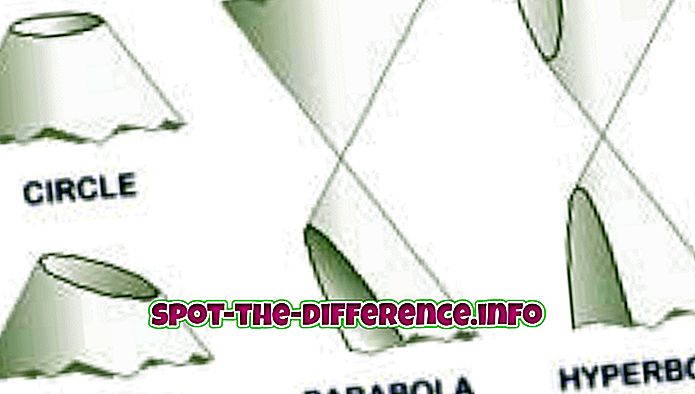
Eine Parabel ist ein konischer Abschnitt, der erstellt wird, wenn sich eine Ebene mit einem Kegel schneidet. Parabeln oder Parabeln bilden "aus dem Schnittpunkt einer geraden kreisförmigen konischen Fläche und einer Ebene parallel zu einer Erzeugungsgeraden dieser Fläche". Eine andere Art und Weise, wie eine Parabel erzeugt wird, besteht darin, dass ein Ort von Punkten auf einer Ebene, die in gleichem Abstand vom Fokus und der Directrix liegen, eine Parabel erzeugt. In der Algebra werden Parabeln häufig in Graphen quadratischer Funktionen verwendet, wobei die Formel y = x ^ 2 verwendet wird.

Eine Linie, die die Parabel durch die Mitte teilt, wird als Symmetrieachse bezeichnet. Diese Linie steht auch senkrecht zur Directrix und verläuft durch den Fokus. Die Punkte, die sich auf der Symmetrieachse befinden und die Parabel schneiden, werden als "Scheitelpunkt" bezeichnet. Der Abstand zwischen dem Scheitelpunkt und dem Fokus wird als 'Brennweite' bezeichnet. Parabolas können in beide Richtungen geöffnet werden, einschließlich nach oben, unten, rechts oder links. Ein Hauptmerkmal von Parabeln ist auch, dass sie alle gleich sind und sich nur in der Größe unterscheiden. Sie können neu positioniert und skaliert werden, um sie an jede andere Parabel anzupassen. Parabolas werden in verschiedenen Anwendungen eingesetzt, z. B. bei Scheinwerfern von Automobilscheinwerfern, beim Entwurf ballistischer Flugkörper usw. Sie spielen auch eine wichtige Rolle in der Physik, im Ingenieurwesen, in der Mathematik usw.

Hyperbeln sind eine glatte Kurve, die auftritt, wenn sich eine Ebene mit dem Kegel parallel zur y-Achse schneidet, die entlang der Seite des Kegels einen Schnitt erzeugt. Eine Hyperbel wird durch ihre geometrischen Eigenschaften oder Gleichungen definiert, für die sie eine Lösungsmenge ist. Der Begriff "Hyperbel" leitet sich vom griechischen Wort ab, was "überschüttet" oder "übertrieben" bedeutet. Man nimmt an, dass der Begriff von Apollonius von Perga geprägt wurde, der einen großen Beitrag zum Studium der konischen Abschnitte geleistet hat.

Eine Hyperbel hat bekanntlich Zweige, die zueinander spiegelbildlich sind und zwei unendlichen Bögen ähneln. Die Punkte auf den beiden am nächsten liegenden Zweigen werden als Scheitelpunkte bezeichnet. Die Linie, die die Scheitelpunkte verbindet, wird als Querachse oder Hauptachse bezeichnet, die dem Hauptdurchmesser einer Ellipse entspricht. Der Mittelpunkt einer Querachse wird als Hyperbola-Zentrum bezeichnet. Die Gleichung einer Hyperbel wird als x2 / a2- y2 / b2 = 1 geschrieben. Hyperbeln werden in der heutigen Welt in verschiedenen Anwendungen verwendet, einschließlich des Pfads, dem der Schatten der Spitze einer Sonnenuhr folgt, die Form einer offenen Umlaufbahn; Es wird als Bogen in vielen gebauten Gebäuden verwendet, als Gleichungen in Mathematik und Geometrie, Physik usw.

Hyperbolas und Parabolas sind beide offene Kurven, was bedeutet, dass sie nicht unendlich enden und unendlich weit gehen, was Ellipsen und Kreise nicht können.